ReinFlow Experiments

What is ReinFlow?

ReinFlow is a general online RL fine-tuning framework for diversee flow matching policies. It is...

🌐 Purely Online: ReinFlow operates entirely online, enabling real-time interaction and adaptation to dynamic environments.
🚀 Inborn Exploration: ReinFlow avoids constraints from pre-trained policies, fostering flexible and innovative exploration.
🛡️ Stable: ReinFlow relaibly improves the reward of pre-trained checkpoints across diverse tasks and random seeds.
⚡ One-Step or Few-Step Fine-Tuning: ReinFlow achieves effective fine-tuning with minimal denoising steps, prioritizing wall-time efficiency at fine-tuning and deployment.
🔄 Versatile: ReinFlow supports multiple flow model variants, such as Rectified Flow with various time distributions, and Shortcut Models.
📘 Theoretically Grounded: ReinFlow’s gradient loss is derived from policy gradient theory for POMDPs, ensuring a solid theoretical foundation.
🧠 General Framework: The algorithm adapts to all pre-trained policies with an ODE path with diverse policy gradient methods.
📂 Reproduceable: We open-source all the training script, hyperparameters, pre-training data, model checkpoints, and training records under the MIT license.

How ReinFlow Works

Routine
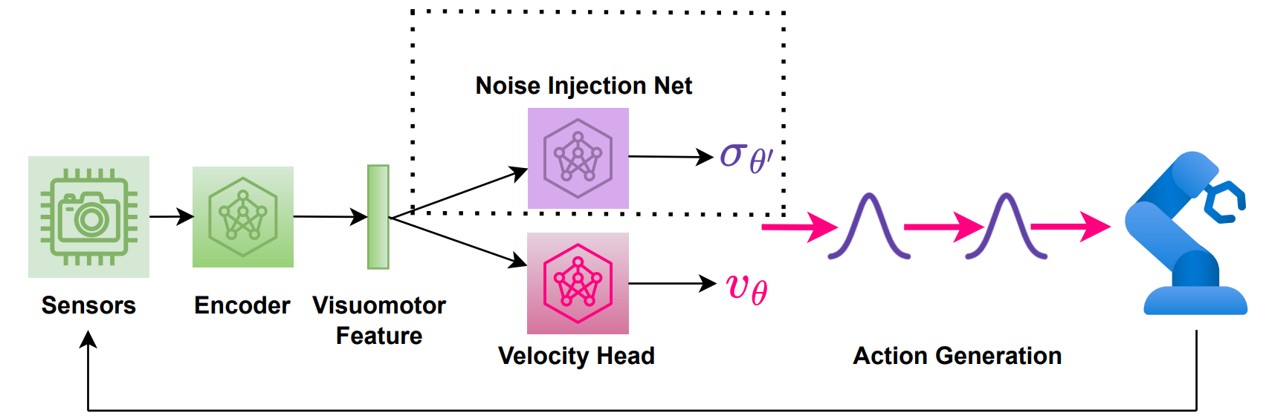
- We provide a pseudocode of fine-tuning flow matching policy with ReinFlow.
  
  ReinFlow
  
  1Input: pre-trained flow's velocity $v_\theta$, denoising step $K$, discount $\gamma$, batch size $B$, discretization scheme $0 = t_0 < t_1 < \ldots < t_K = 1$ with $\Delta t_k := t_{k+1} - t_k$, regularizor $\mathcal{R}$ with intensity $\alpha \in \mathbb{R}$.
  
  2While not converged:
  
  3Restore $\bar{\theta}_{\mathrm{old}} \leftarrow \mathrm{stop\_grad}([\theta, \theta'])$.
  
  4Reset env, receive observation $o$.
  
  5While not done:
  
  6Sample $a^0 \sim \mathcal{N}(0, \mathbb{I}_{d_A})$.
  
  7For denoising step $k \in \{0, 1, \ldots, K-1\}$:
  
  8$a^{k+1} \leftarrow a^k + v_\theta(t_k, a^k, o) \Delta t_k + {\color{purple}{\sigma_{\theta'}(t_k, a^k, o)}} \epsilon$, where $\epsilon \sim \mathcal{N}(0, \mathbb{I}_{d_A})$.
  
  9Play action $a = a^K$, receive reward $r$ and done flag $d$, update observation $o$.
  
  10Store $\{\mathbf{a}, o, r, d\}$ to buffer, where $\mathbf{a} := (a^0, a^1, \ldots, a^K)$.
  
  11Sample $\{\mathbf{a}_i, o_i, r_i, d_i\}_{i=1}^B$ from buffer.
  
  12Compute transition probability for all denoising step $k$ and tuple $i$:
  
  13
  \[{\color{purple}{\ln \pi^{\bar{\theta}}\left(a_i^{k+1} | a_i^k, o_i\right)} = \ln \mathcal{N}\left(a_i^{k+1} \mid a_i^k + v_\theta(t_k, a_i^k, o_i) \Delta t_k\ , \ {\color{purple}{\sigma_{\theta'}^2(t_k, a_i^k, o_i)}}\right)}\]
  
  14Estimate advantage $A^{\bar{\theta}_{\mathrm{old}}}$ by a sub-routine and jointly optimize $\theta$ and $\theta'$ by
  
  15
  \[\begin{aligned}\theta, \theta' = \underset{\theta, \theta'}{\mathrm{argmin}} \frac{1}{B} \sum_{i=1}^B \Big[ & -A^{\bar{\theta}_{\mathrm{old}}}(o_i, a_i) {\color{purple}{\sum_{k=0}^{K-1} \ln \pi^{\bar{\theta}}\left(a_i^{k+1} | a_i^k, o_i\right)}} + \alpha \cdot \mathcal{R}\left(\mathbf{a}_i, o_i; \bar{\theta}, \bar{\theta}_{\mathrm{old}}\right) \Big]\end{aligned}\]
  where $\bar{\theta} := [\theta, \theta']$.
  
  16Return: fine-tuned flow policy's velocity $v_\theta$.
Structure of the Noise:
- Zero-mean: The noise injected is a magnitude-modulated centered Gaussian noise, matching the dimensions of the actions.
- Bounded:
  - Bounded noise is adopted to avoid exceeding physical constraints (too large) or limiting exploration (too small).
  - Implementation: Noise net output is squeezed through a tanh function, then scaled and shifted to a desired region.
  - Upper and lower bounds are hyperparameters relevant to the robot embodiment.
  - During fine-tuning, the noise net searches within these bounds and naturally decays as the policy converges to a high success rate.
  - Entropy regularization may increase noise to promote exploration.
- Learnable: Conditioning noise on denoising time, denoised action, and observation improves performance, with minimal parameter increase during fine-tuning (compared to constant noise).
- Markovian: Noise depends only on the current denoised action, not previous ones, ensuring the joint probability expands into the sum of transition probabilities.
Parameter Efficiency: The noise network shares features with the velocity head, increasing success rate with minimal parameter increase during fine-tuning.
After Fine-Tuning: The noise network is discarded, and the fine-tuned model uses ODE inference for fast generation.

Input Type	Reward Type	Environment	Data Source
State	Dense	OpenAI Gym	D4RL data
State	Sparse	Franka Kitchen	Human-teleoperated data from D4RL
Visual	Sparse	Robomimic	Human-teleoperated data processed like DPPO's paper

2. Performance Evaluation and Comparisons

2.1 Comparison with DPPO and FQL

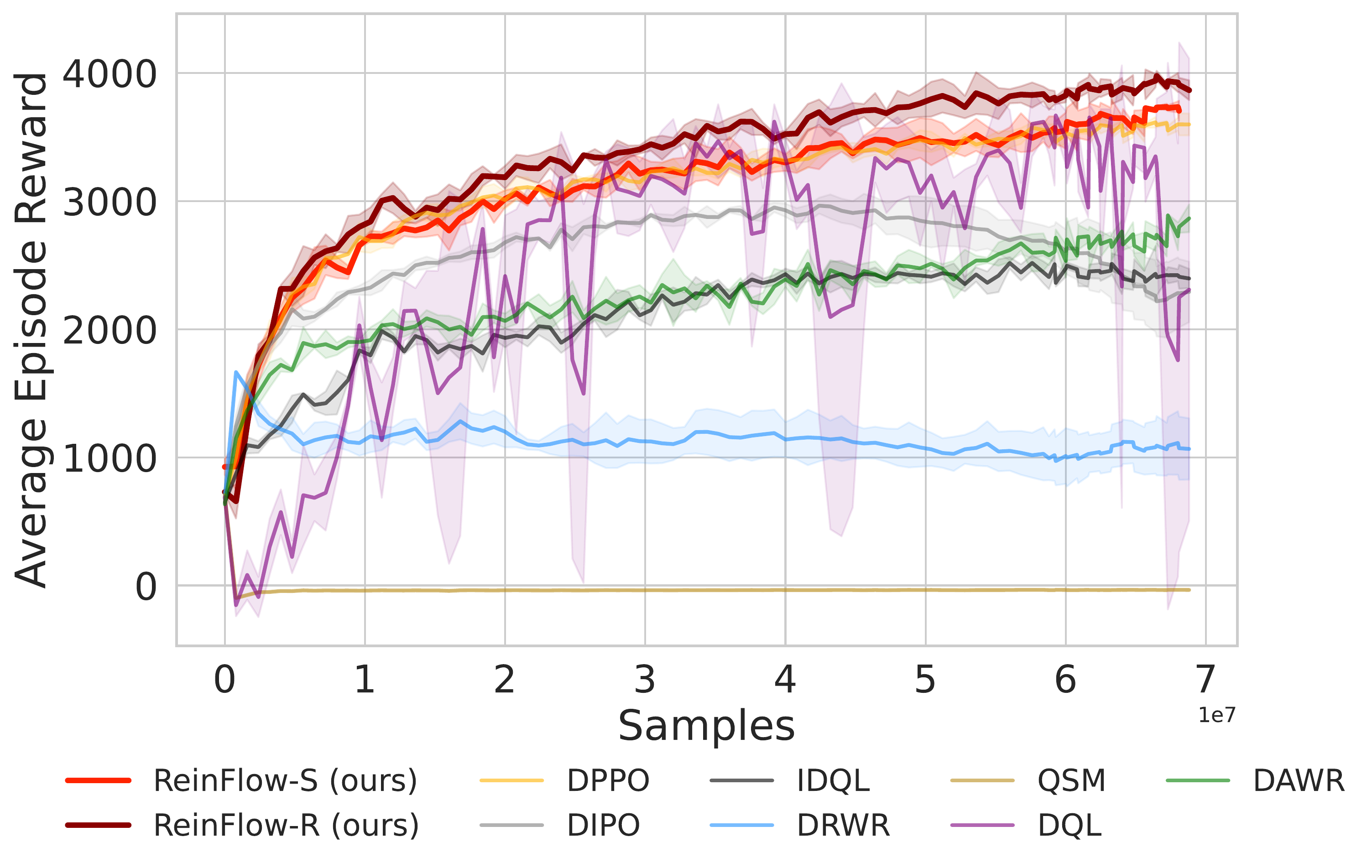
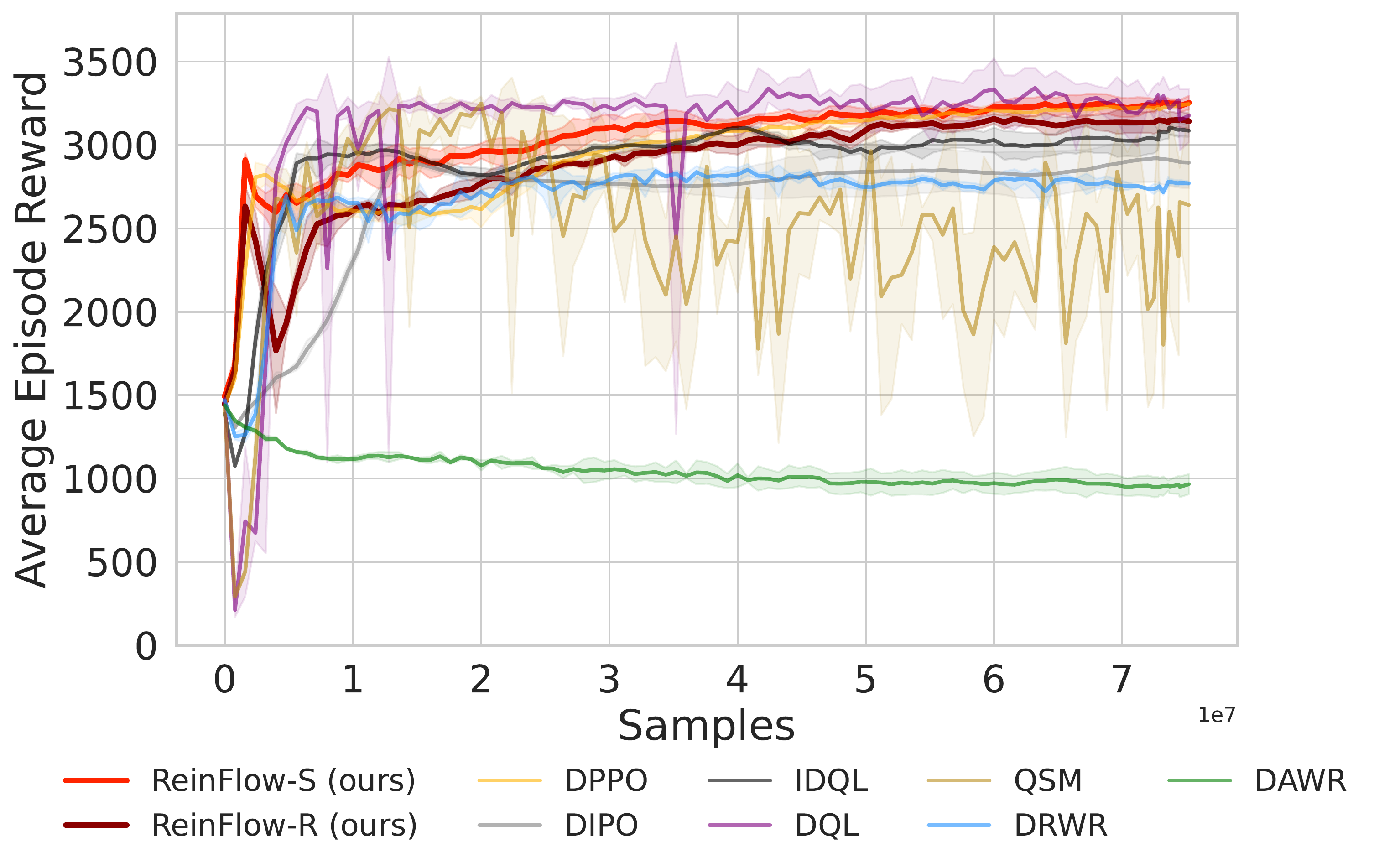
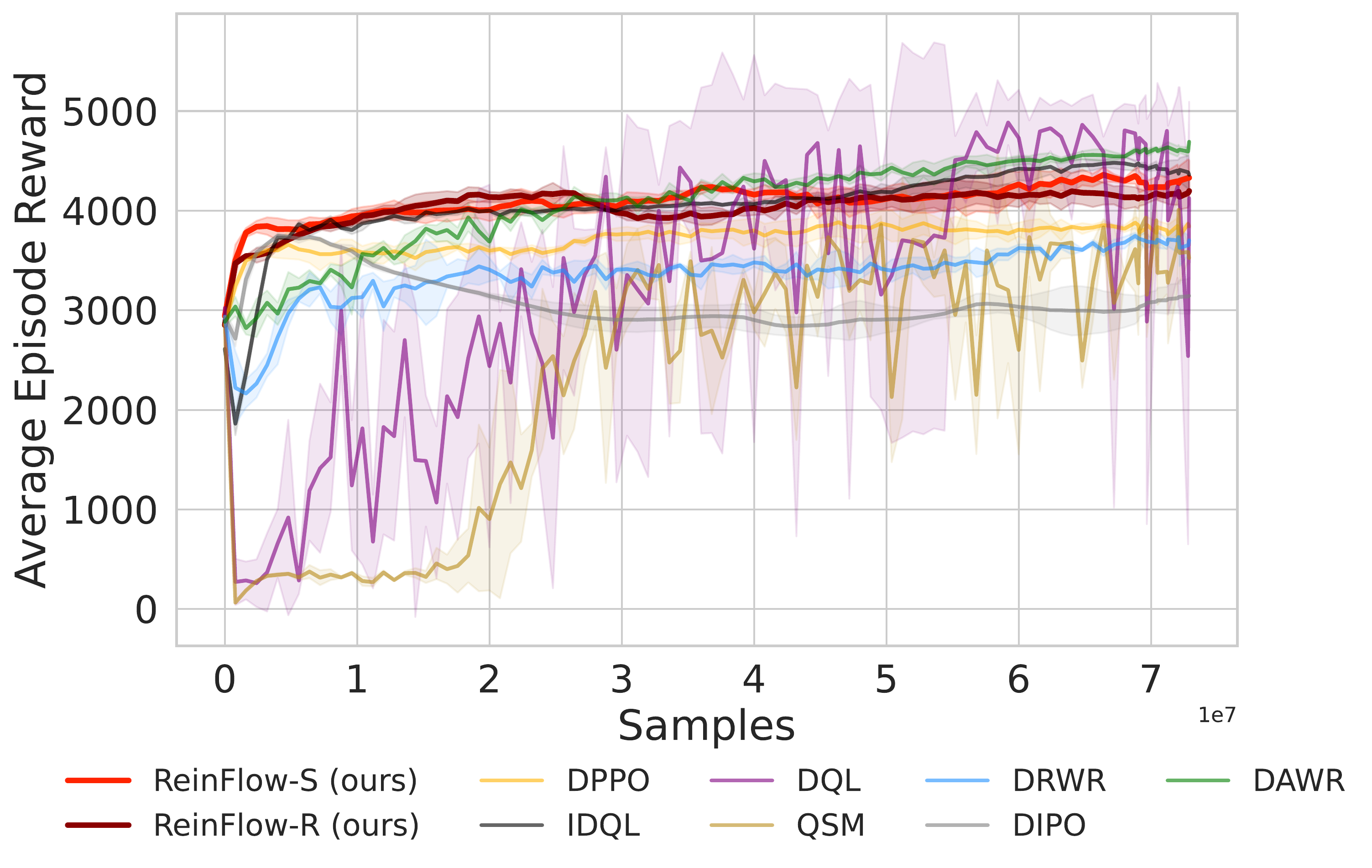
📈 ReinFlow consistently enhances performance across Gym and Franka Kitchen benchmarks, boosting success rates by 40.09% in Robomimic tasks with fewer steps than DPPO.

(A) Hopper-v2

(B) Walker-v2

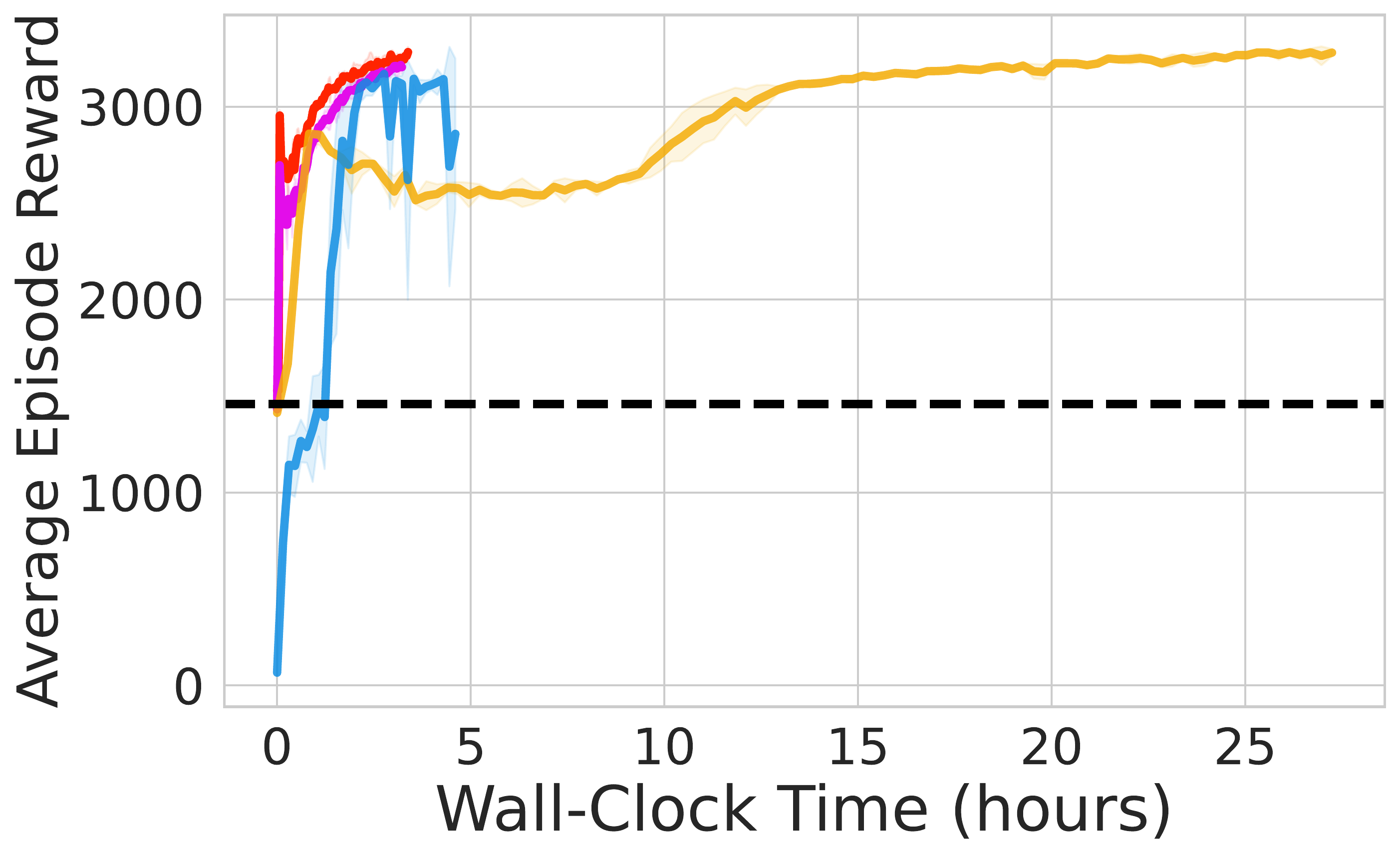
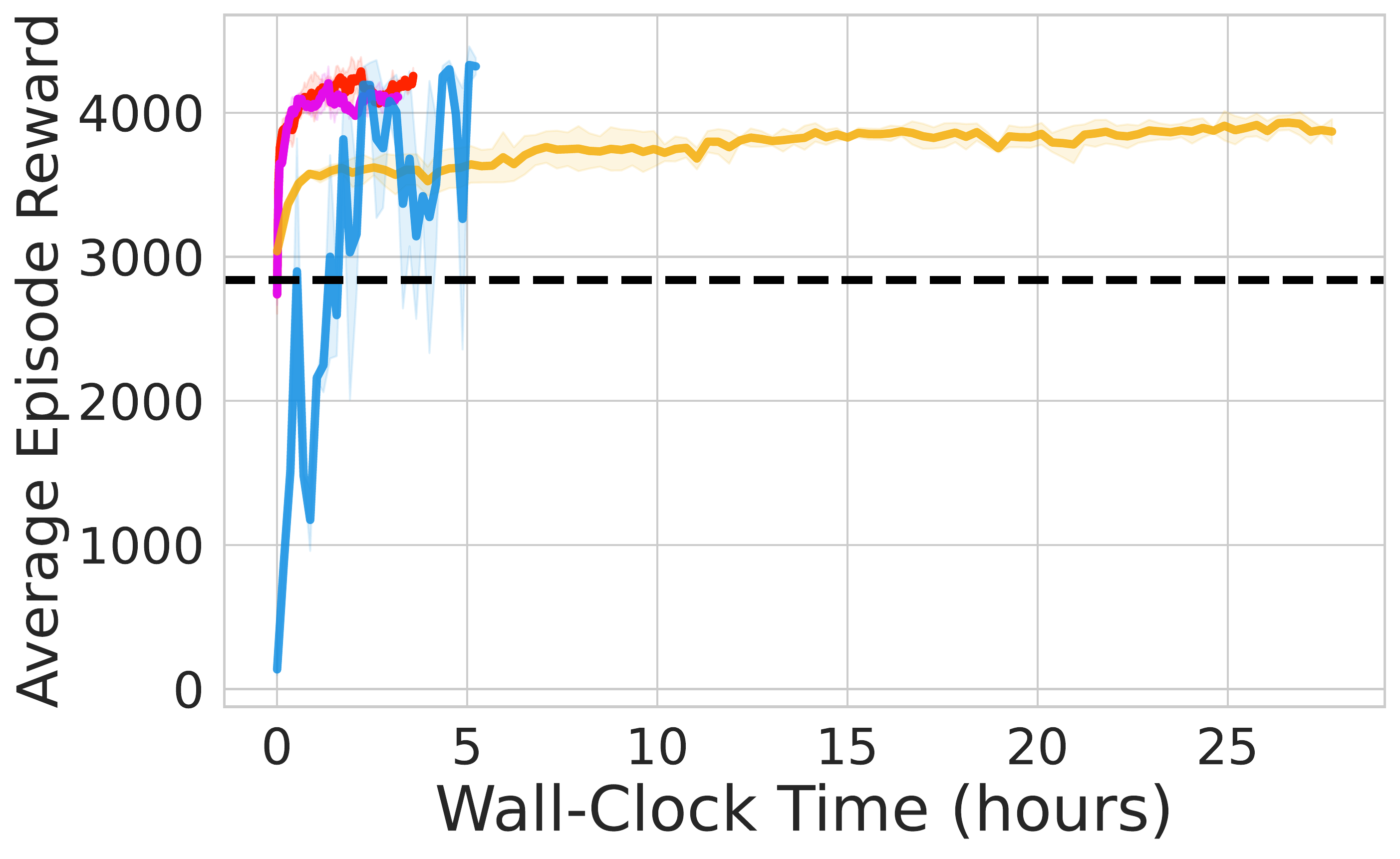
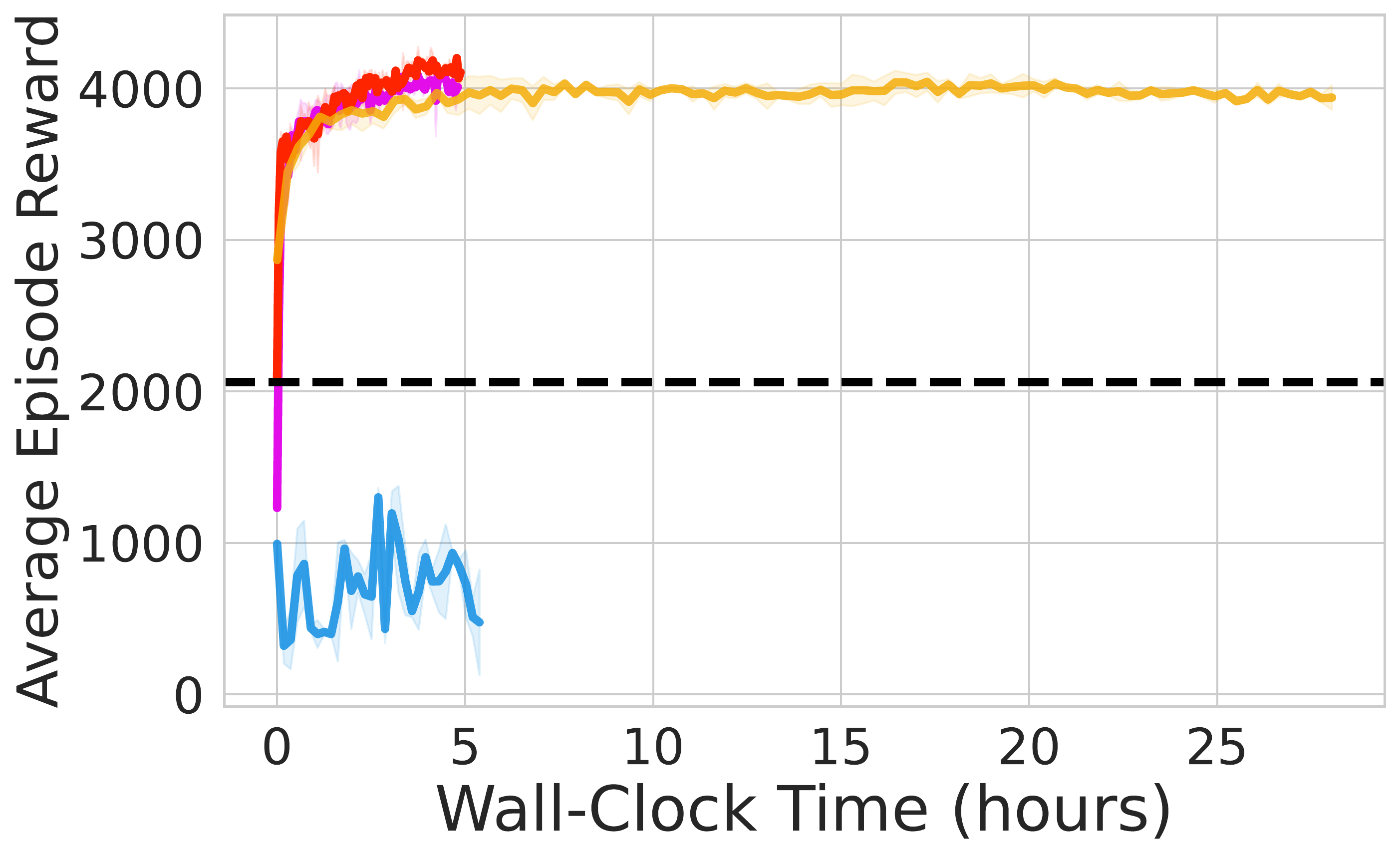
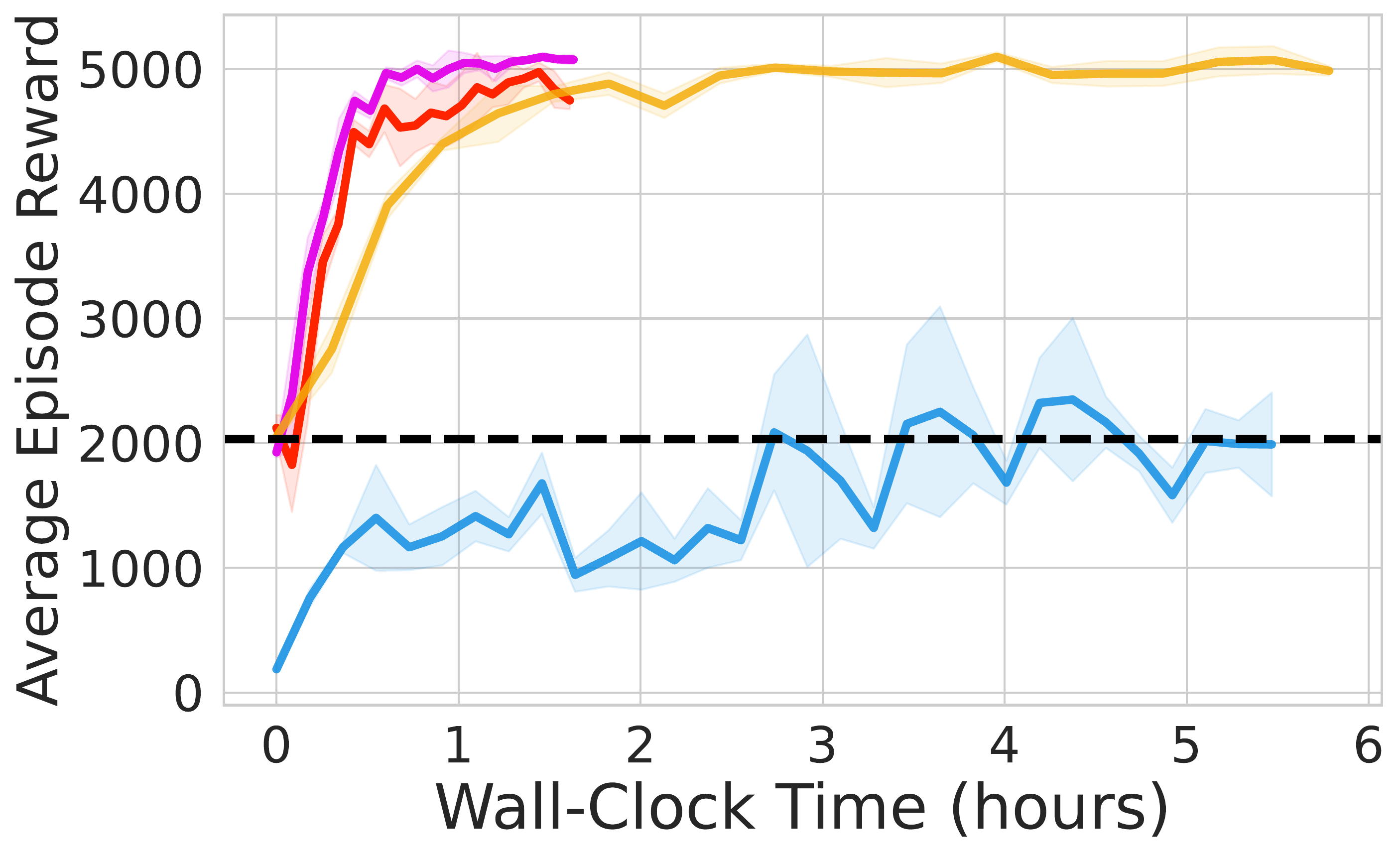
(D) Humanoid-v3

Wall time efficiency results of state-based locomotion tasks in OpenAI Gym. Dashed lines indicate the behavior cloning level.

(A) Kitchen-complete

(B) Kitchen-complete

(D) Kitchen-partial

Task completion rates of state-input manipulation tasks in Franka Kitchen. (A) and (B) show the completion rates against the wall time and sample cost. We only show the sample cost plots for agents trained on mixed and partial datasets for brevity.

(A) Can

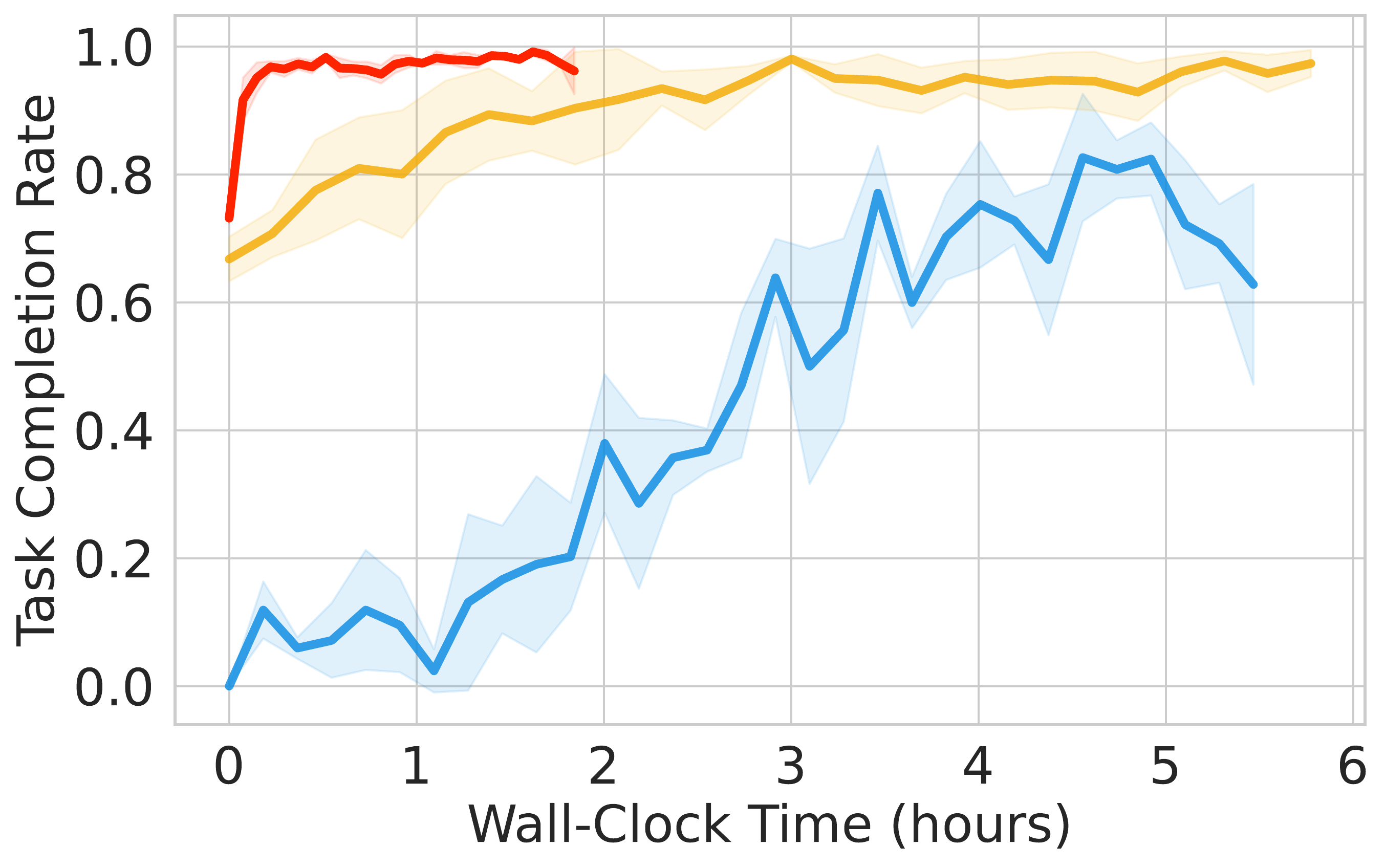
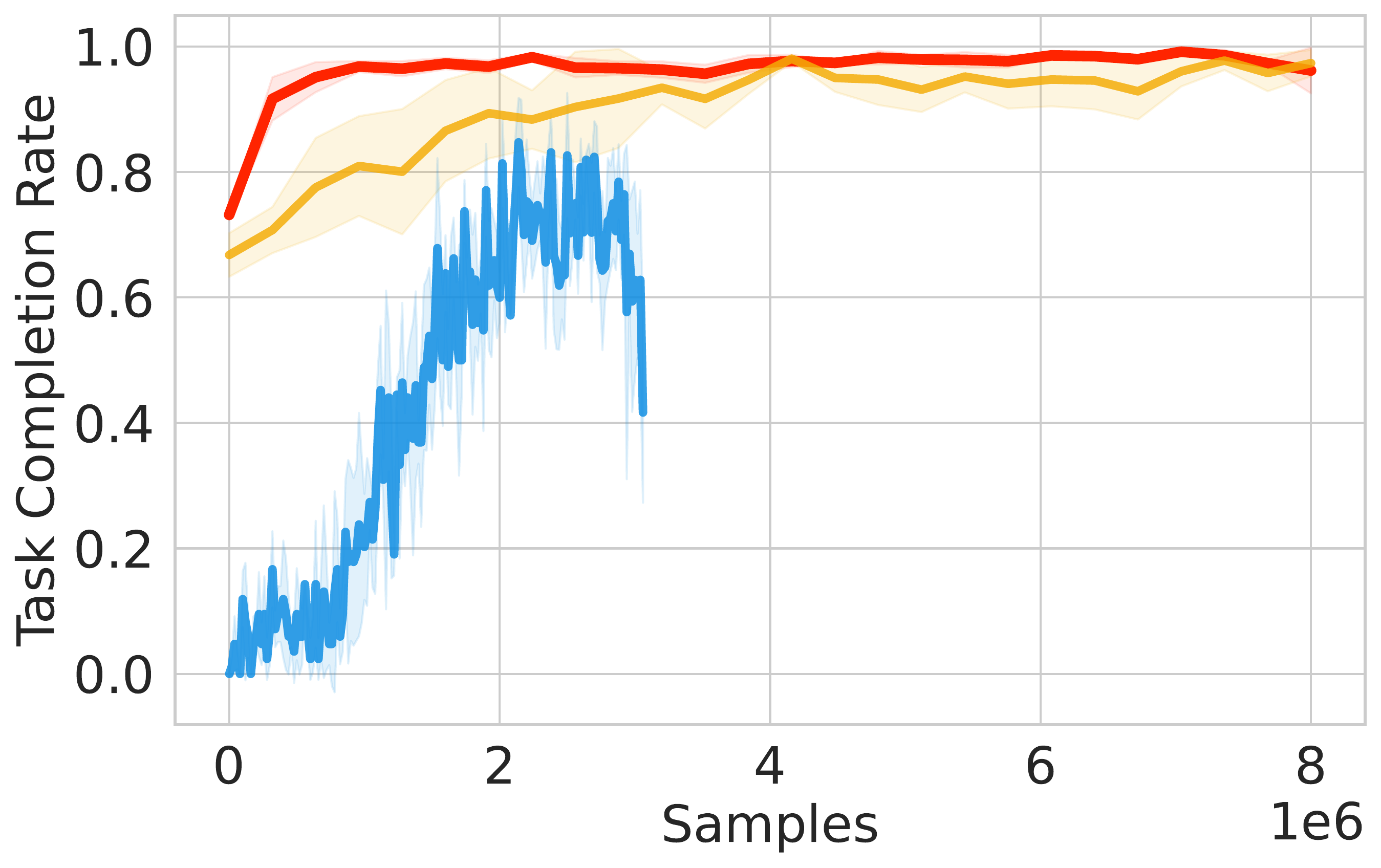
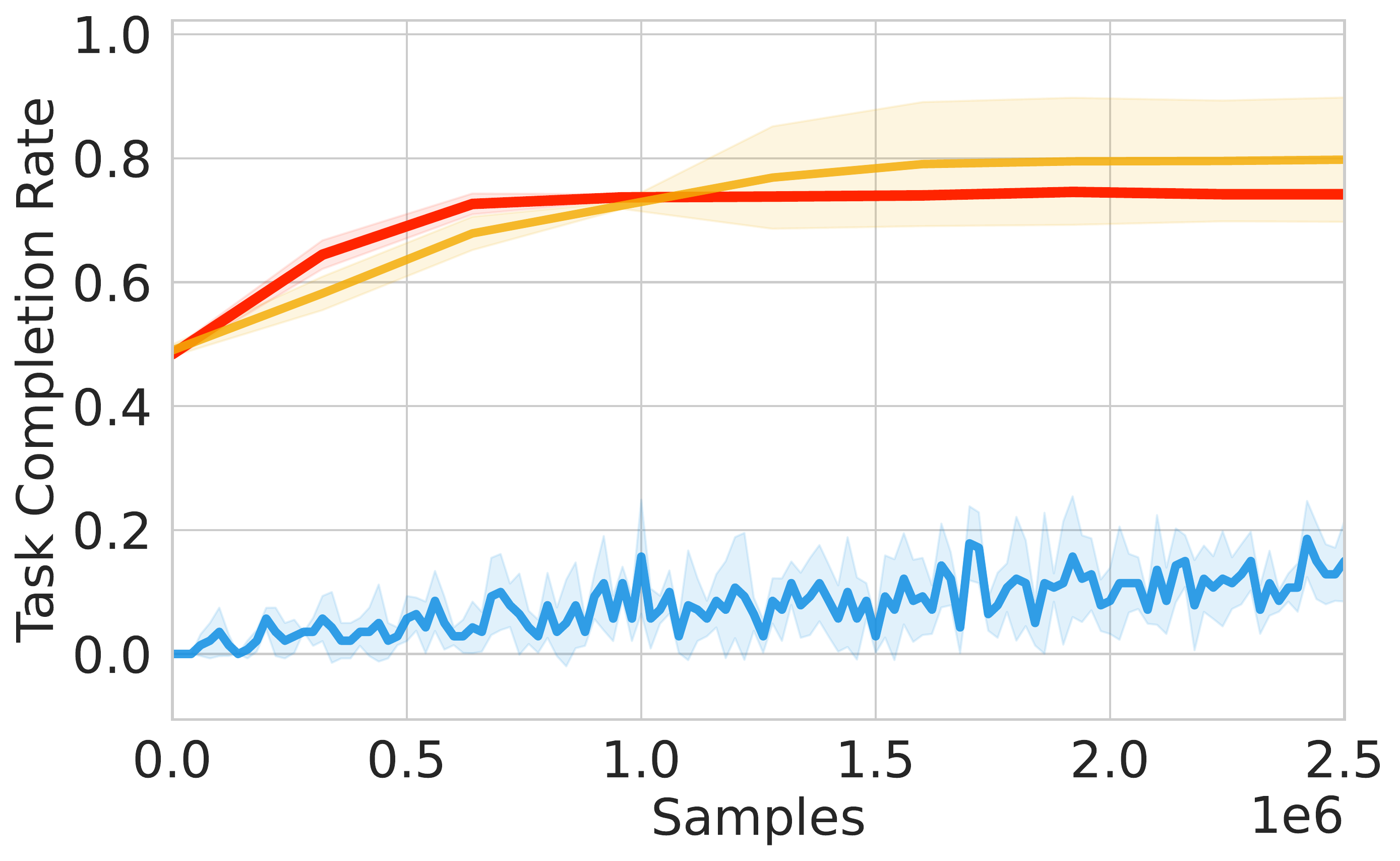
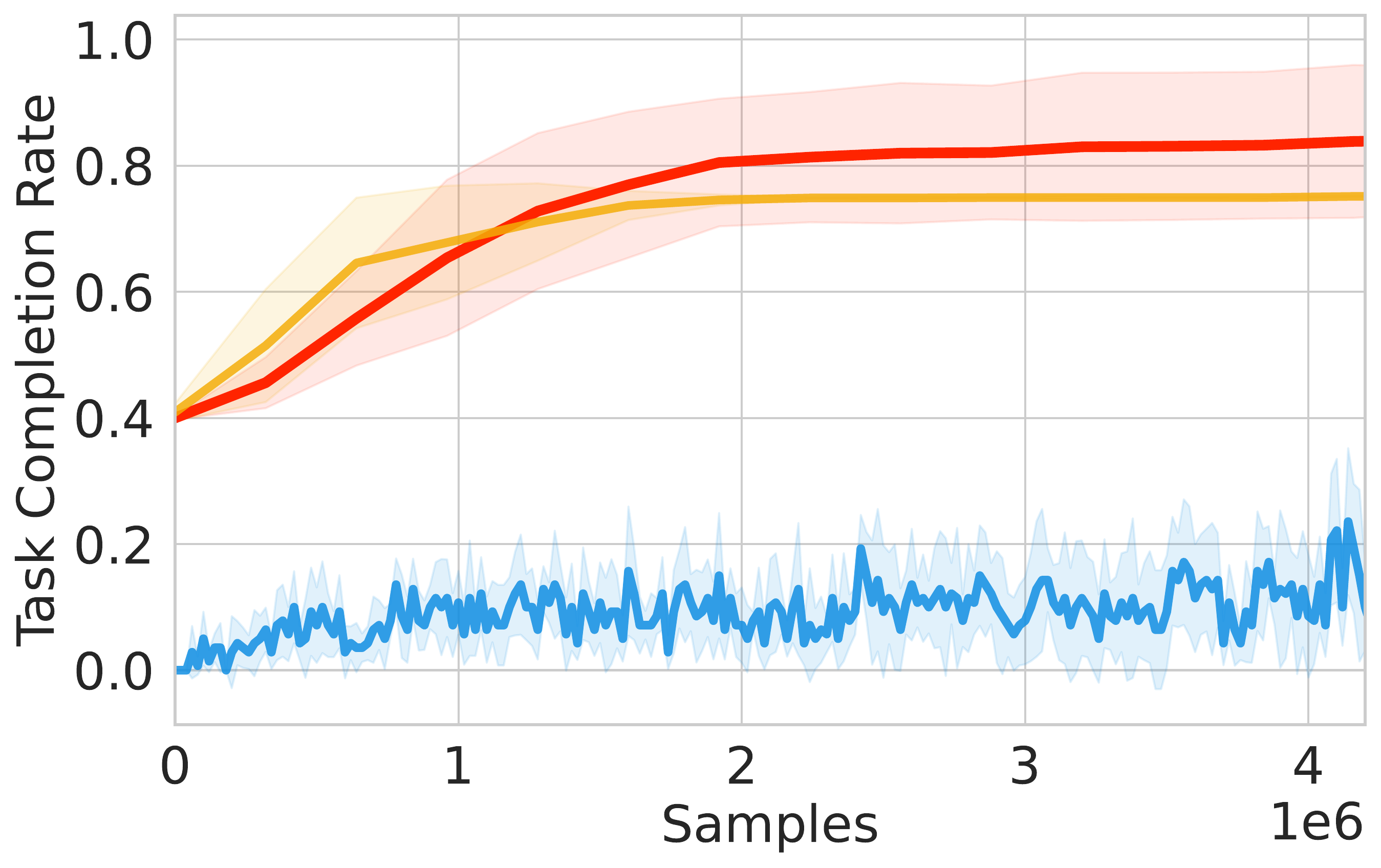
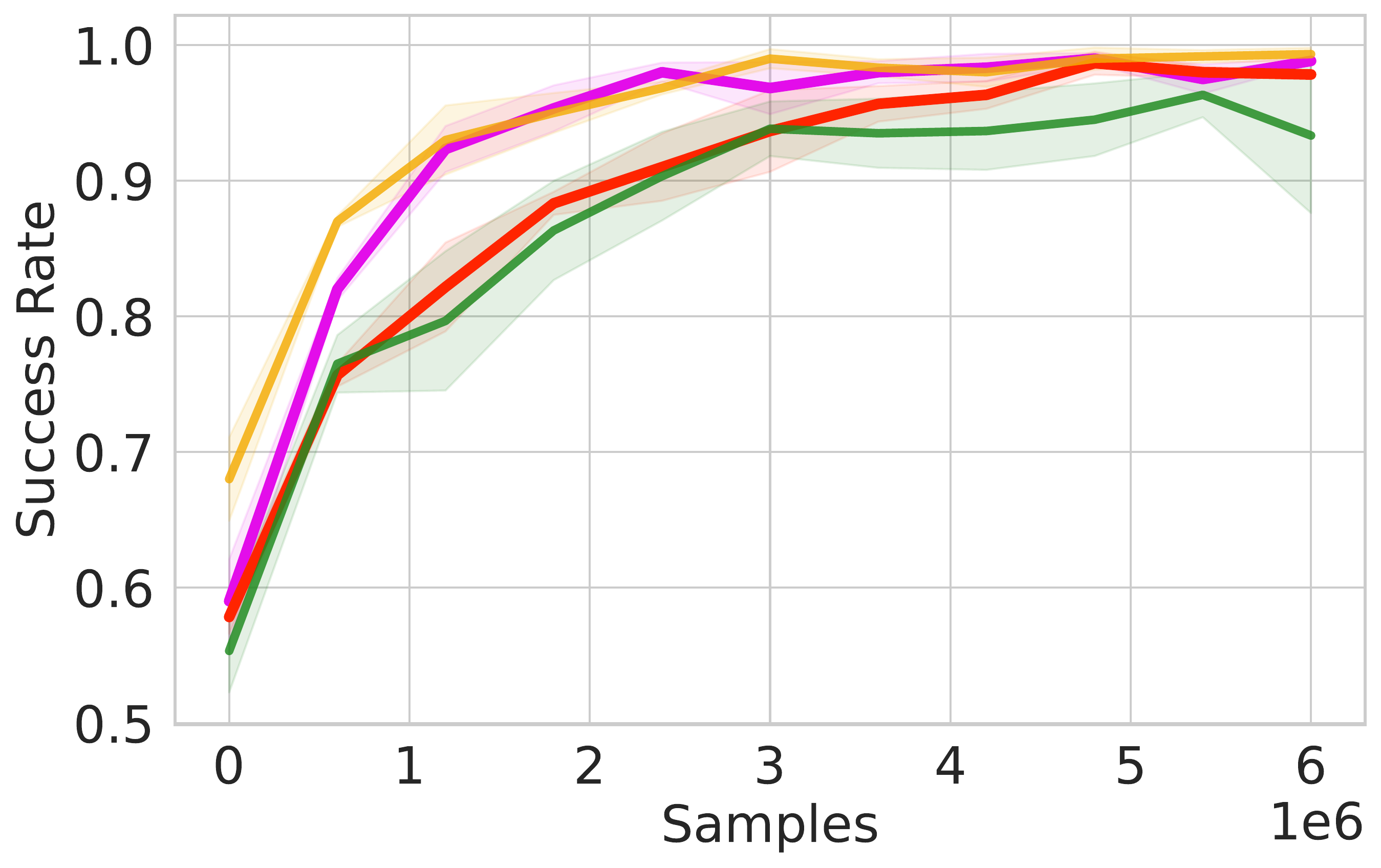
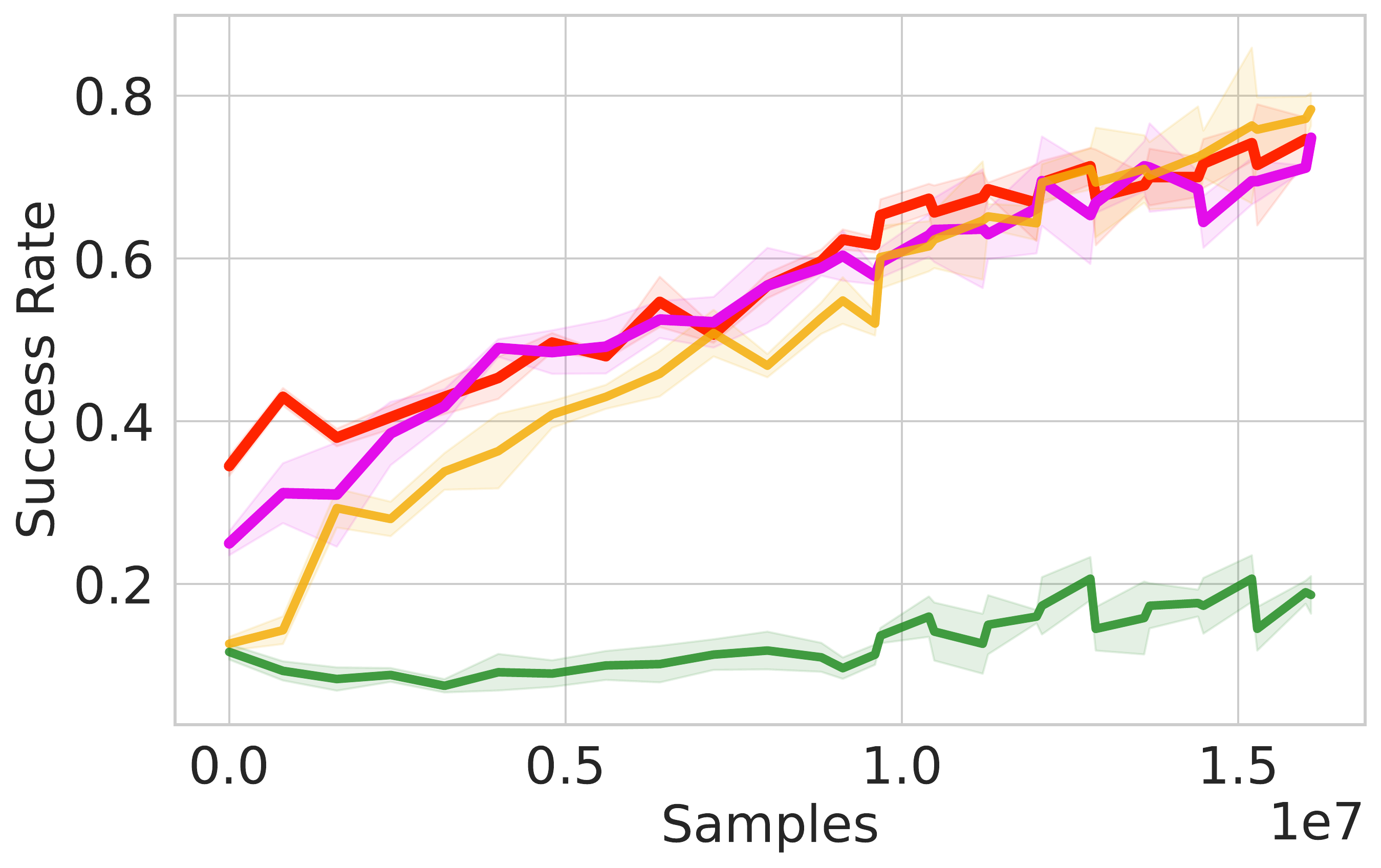
(B) Square

Success rates in visual manipulation tasks in Robomimic.

2.2 Comparison with Other Diffusion RL Methods

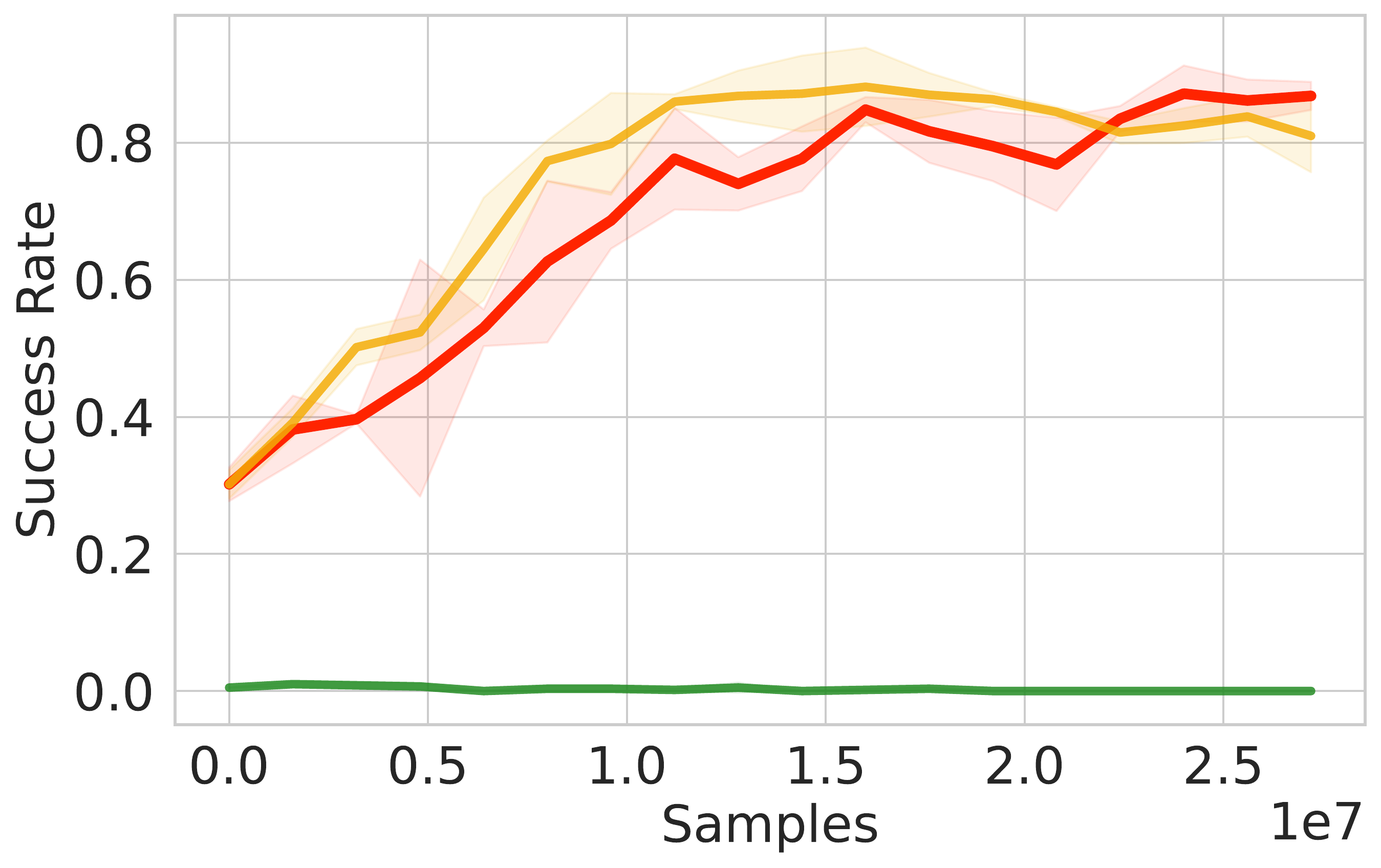
⚖️ ReinFlow outperforms diffusion RL baselines in stability and asymptotic performance across continuous control tasks like Ant-v0, Hopper-v2, and Walker2d-v2.

📊 Using consistent hyperparameters from prior work, ReinFlow demonstrates superior performance, as shown in Fig. 5(A-C).

(A) Ant-v0

(B) Hopper-v2

Fine-tuning locomotion tasks Ant-v0, Hopper-v2, and Walker2d-v2 with Diffusion RL baselines and ReinFlow.

3. The Design Choice and Key Factors Affecting ReinFlow

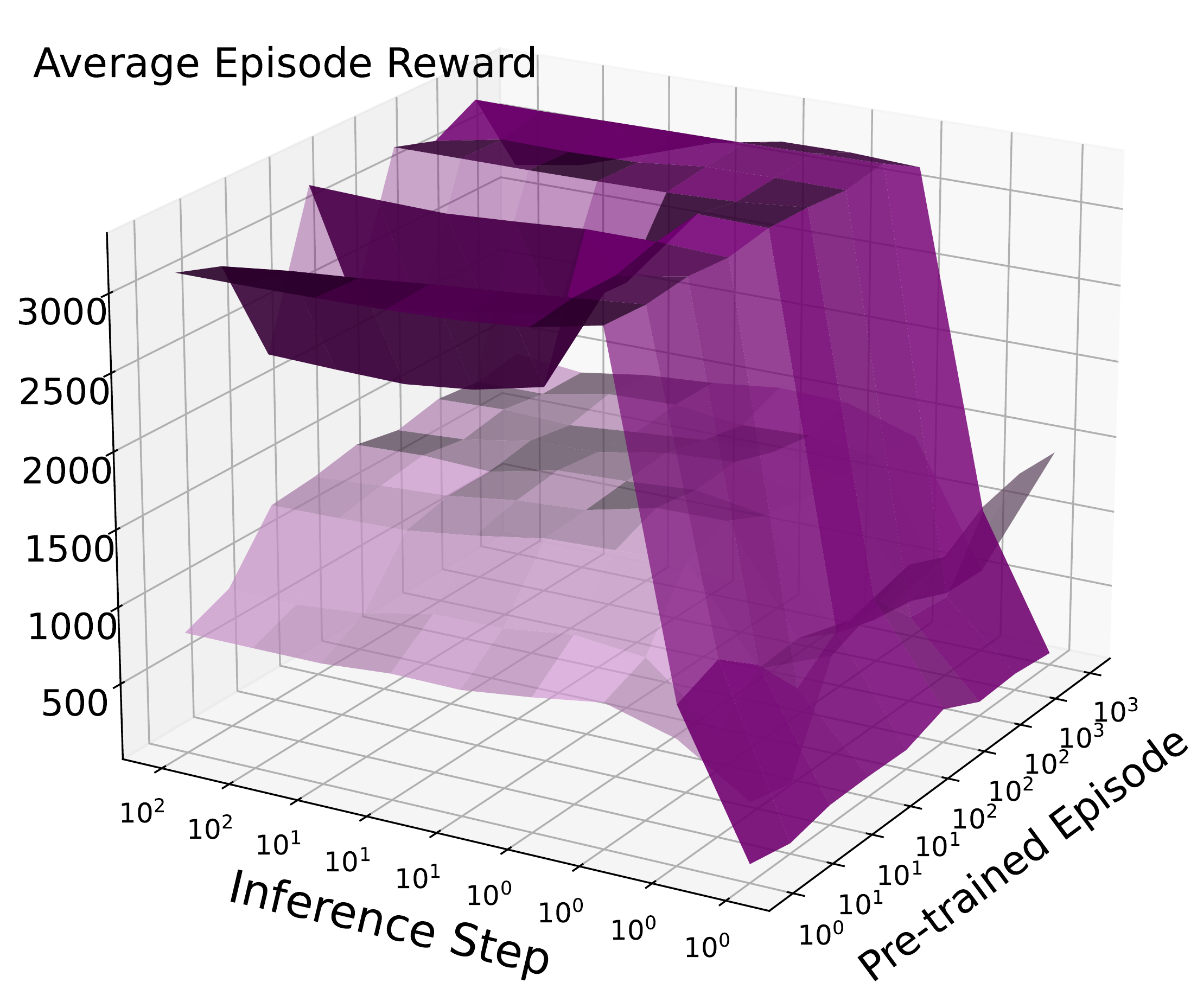
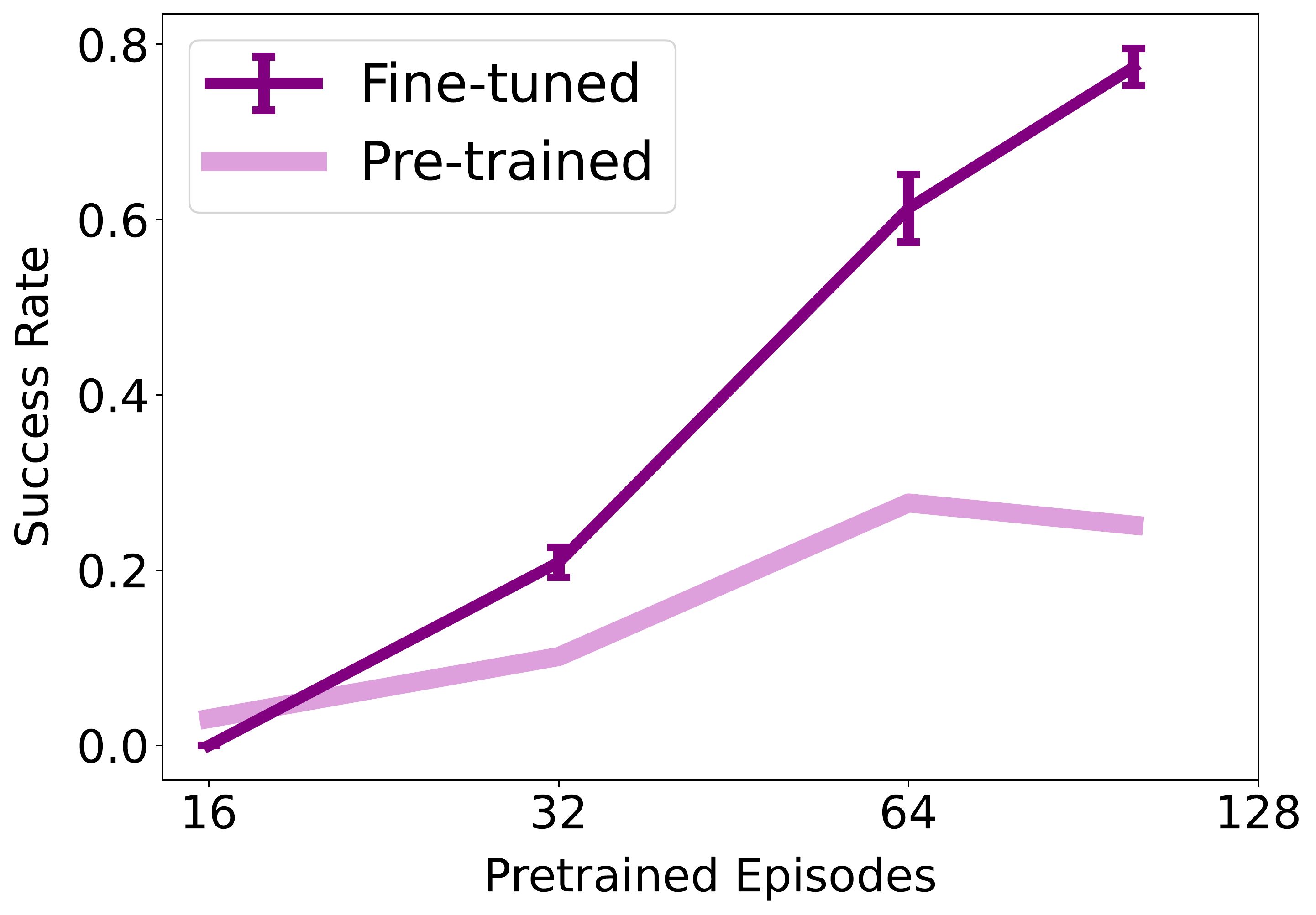
We examine how pre-trained models, denoising steps, noise levels, regularization and denoising step number impact ReinFlow.

3.1 RL Provides Another Scaling Dimension

➖ Scaling data or inference steps: quickly plateaus.

📈 Fine-tuning with RL (ReinFlow): consistently enhances performance.

(A) ReFlow Policy in Hopper-v2

(B) Shortcut Policy in Square

RL provides another way of scaling apart from increasing pre-training data and inference consumption, which has a plateauing effect. The improvement is invariant of flow policy’s time distribution and is achievable at four steps in Hopper (A) and one step in Square (B, C).

3.2 Flow Matching's Time Distribution

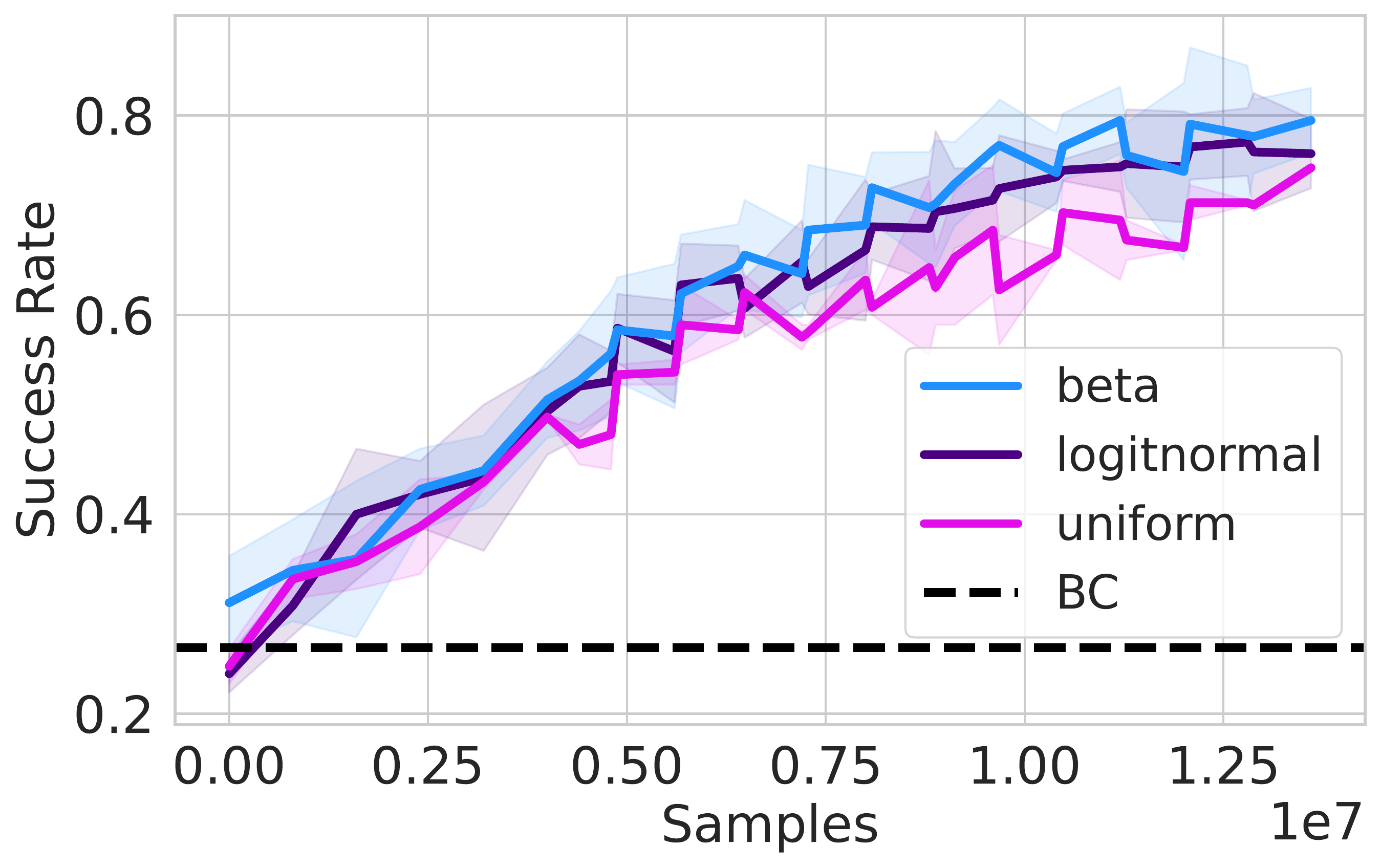
ReinFlow's performance is robust to changes in time sampling.

✅ Uniform

✅ Logit-normal

✅ Beta (slightly better for single-step fine-tuning.)

3.3 Noise Network Inputs

Conditioning noise on state alone works well.

Conditioning noise on both state and time generates more diverse actions and improves success rates.

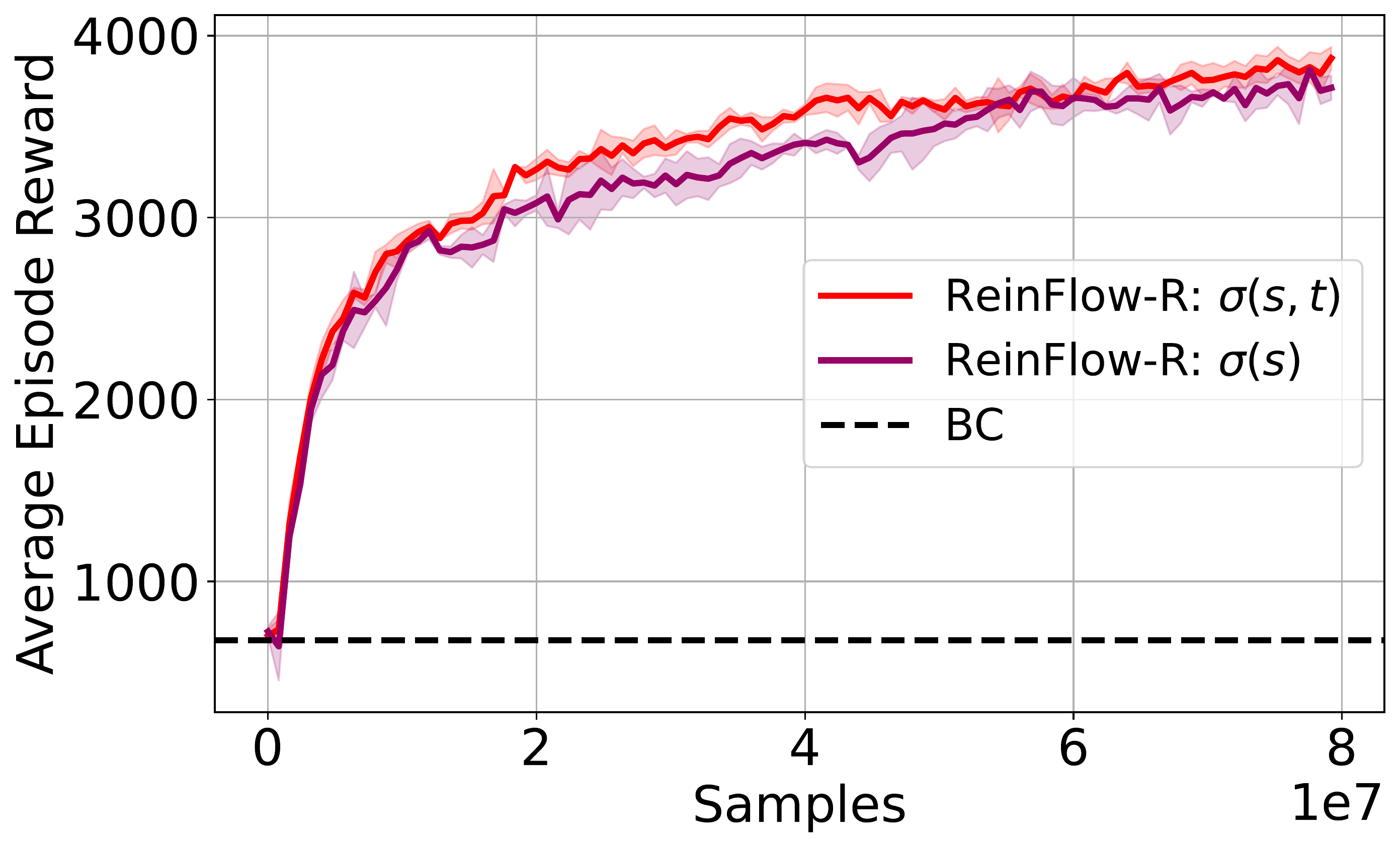
(A) Noise Input's Effect in Ant-v0

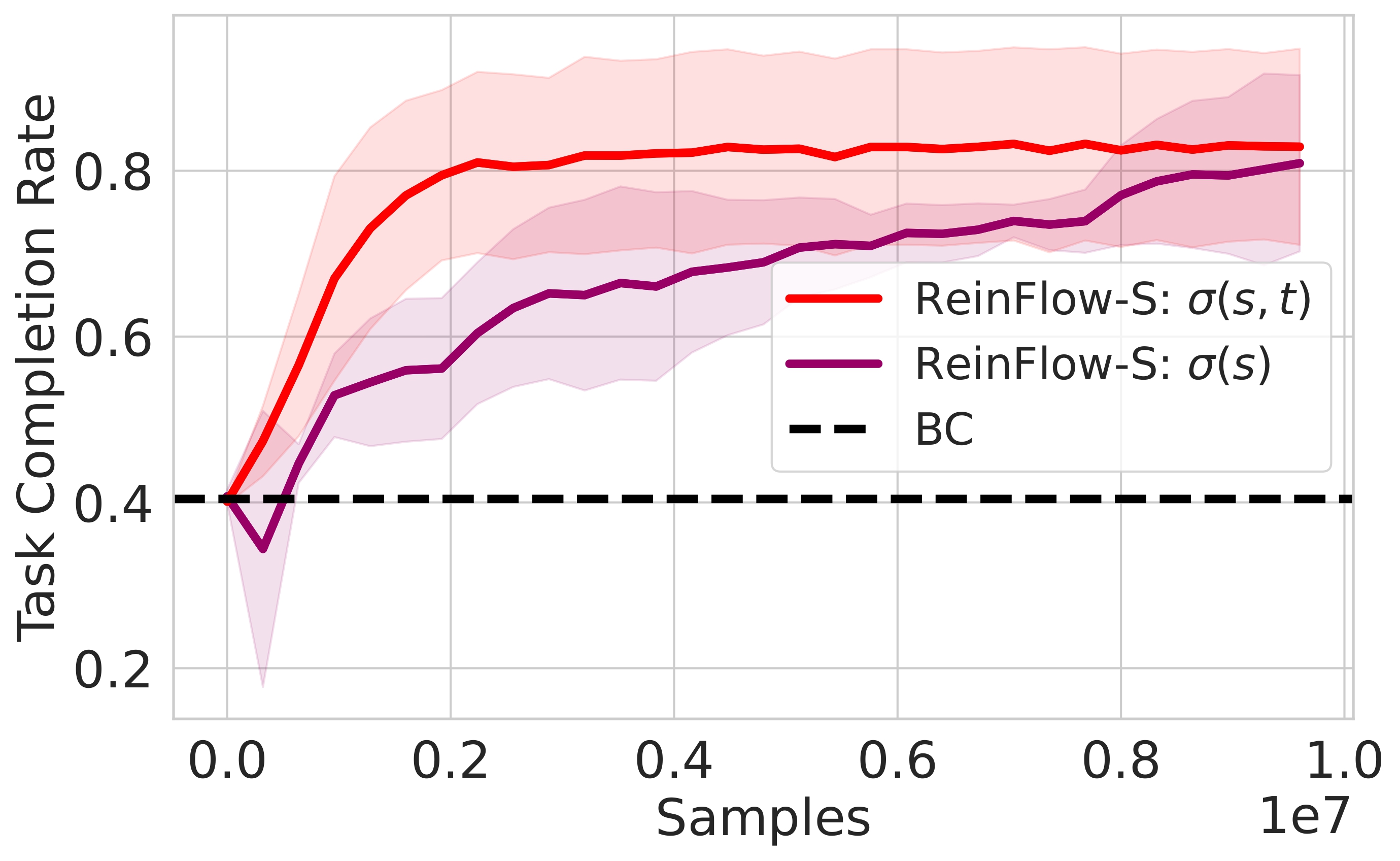
(B) Noise Condition's Effect in Kitchen-partial-v0

Conditioning on state and time yields a higher success rate than only conditioning on states.

3.4 Noise Level and Exploration

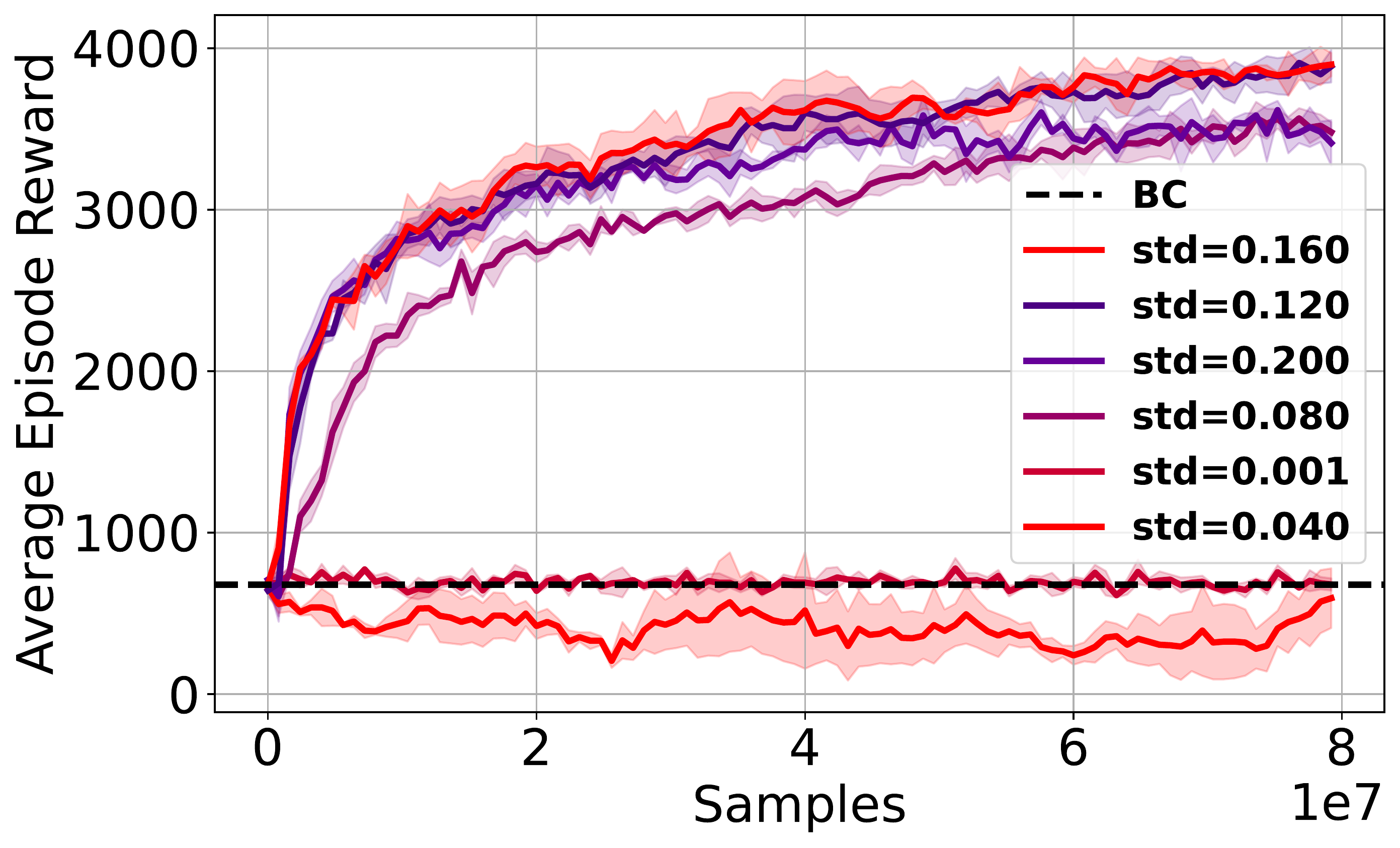
⚖️ Noise magnitude affects exploration: too little traps the policy, too much hurts execution.

🚀 Optimal noise levels enable significant gains, especially in complex tasks.

🔒 Policies become less sensitive to noise once in the correct region.

3.5 Regularization and Exploration

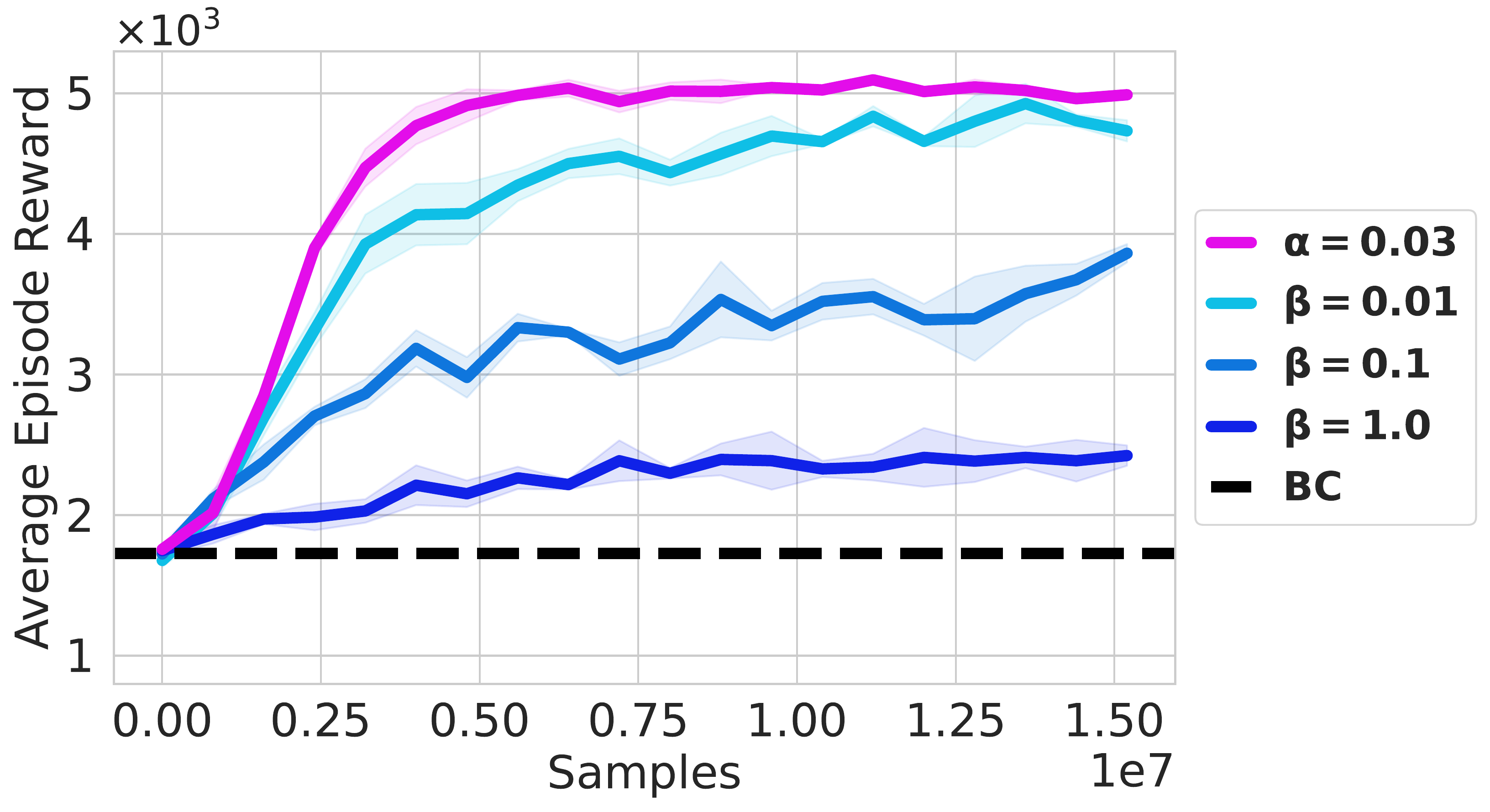
🏅 Entropy regularization promotes exploration, while behavior cloning regularization can trap the policy and is unnecessary.

🏅 Entropy regularization outperforms Wasserstein-2 constraints used in offline RL methods like FQL.

(A) Noise Level Affects Exploration in Ant-v0

(B) Regularization Affects ReinFlow in Humanoid-v3

Noise level and regularization's effect. (A) demonstrates constant noise with different standard deviation affects ReinFlow's exploration. (B) shows how entropy regularization with coefficient $\alpha$ and $W_2$ regularization with different coefficients $\beta$ influences ReinFlow.

3.6 The Number of Denoising Steps

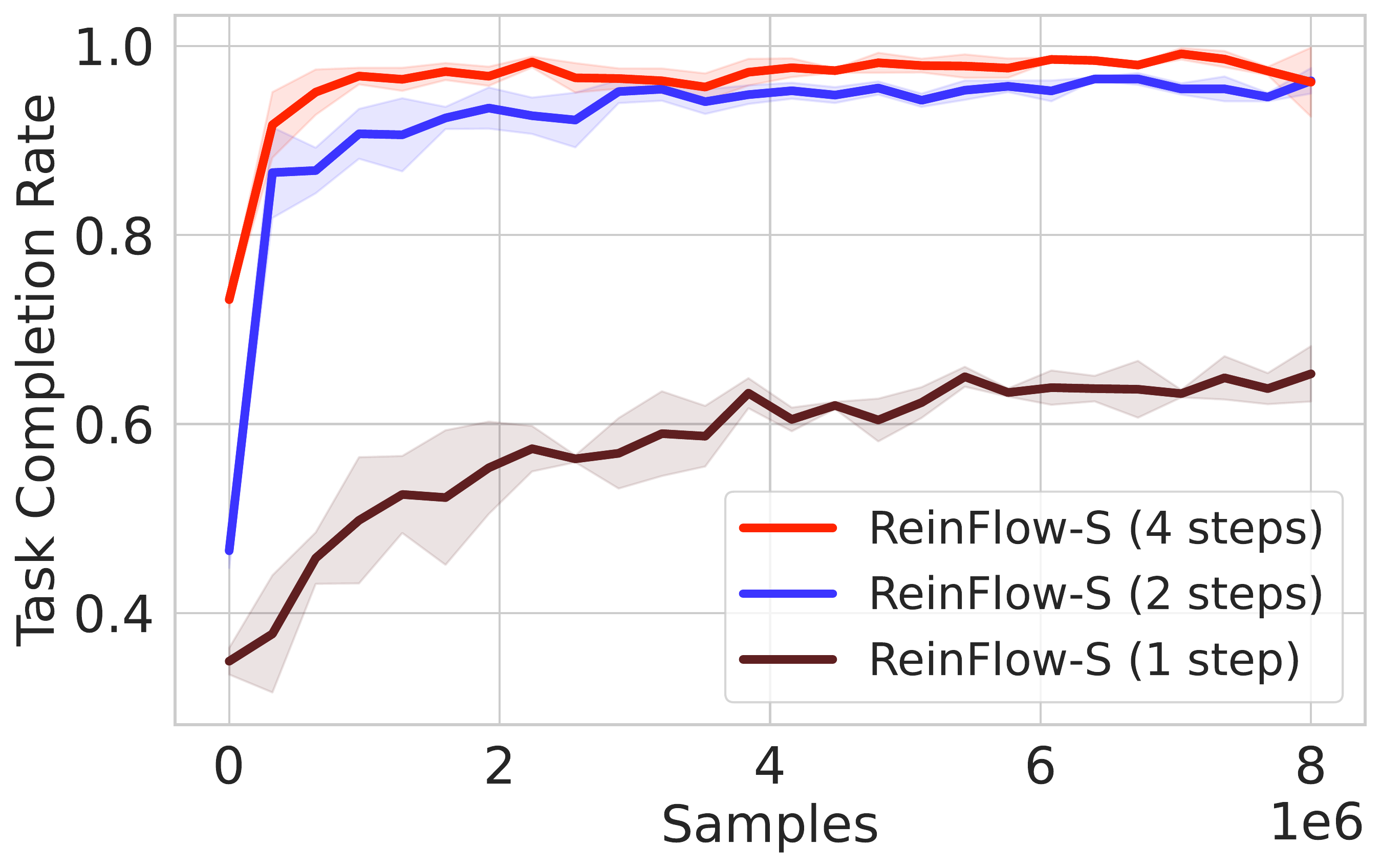
📈 Increasing the number of denoising steps $K$ in ReinFlow boosts initial rewards in Franka Kitchen’s Shortcut Policy but results in rapid reward plateaus, as shown in Fig. 4(A).

🎯 In visual manipulation tasks, lowering noise standard deviation with higher $K$ improves performance for pre-trained policies with low success rates.

(A) Denoising Steps in Kitchen-complete

Fine-tuning Shortcut Policy in Kitchen-complete-v0 at denoising steps $K=1,2,4$, averaged over three seeds (0, 42, 3407).

Common Questions about ReinFlow

In which space is the noise added, and what does it mean physically?
- Noise is added in the virtual denoising process, not directly to the final (real) action.
- Noise injection equates to slightly adjusting joint angles during action generation.
- Noises ultimately influence the real action deployed in the environment.

Flow models have an exact probability expression, why not use it directly?

Flow models' exact solution, \[ \ln p_1(\psi_1(x)) = \ln p_0(\psi_0(x)) - \int_0^1 \nabla \cdot v(t, \psi_t(x)) \, \mathrm{d}t, \quad x \sim p_0(\cdot), \] requires approximation in practice: \[ \widehat{\ln p_1}(x_1) = \ln p_0(x_0) - \sum_{k=0}^{K-1} \mathrm{tr}\left[Z^\top \partial_X v_\theta(t_i, X_{t_i}) Z\right] \Delta t_i, \] where $ Z \sim p_Z(\cdot) $, $ \mathbb{E}[Z] = 0 $, $ \mathrm{Cov}[Z] = \mathbb{I}_{d\times d} $. This introduces Monte-Carlo noise and simulation errors.
ReinFlow directly treats the inference as a discrete-time process, avoiding discretization errors and working with very few steps.
ReinFlow adds bounded Gaussian noise, so the statistics of denoised actions is simple to compute and fully known, eliminating the Monte-Carlo errors in trace estimate.

Aspect	Naïve Approach (no noise injection)	ReinFlow
Noise Type	Directly compute log probability	Inject learnable noise
Error	Unknown Monte-Carlo and discretization error	Controllable and fully known Gaussian noise
Accuracy	Inaccurate at few steps	No discretization concerns, accurate for 4, 2, or 1 steps
Computation	Compute-intensive in multiple steps	Fast closed-form solution

Why add structured noise?
- Smooths the ODE for a simple and exact likelihood expression, vital for reinforcement learning (RL).
- Enables controllable exploration during fine-tuning through pre-defined and adjustable bounds, as well as regularization.
What is the ReinFlow related to ODE-SDE conversion? When the denoising step count is large enough, ReinFlow can be viewed as augmenting the pre-trained flow ODE to a non-linear stochastic differential equation, which enhances generation diversity and exploration.
\[ \begin{align} \text{SDE general form:}\ \ \qquad \ \ \mathrm{d}X_t &= \quad f(X_t, t) \ \ \ \mathrm{d}t \ \ + \qquad {\color{purple}{ \sigma(X_t, t) }} \, \mathrm{d}W_t \\ \text{ReinFlow's update:}\ \ a^{k+1} - a^k &= \underbrace{v_\theta(t_k, a^k, o) \Delta t_k}_\text{Drift} + \underbrace{{\color{purple}{ \sigma_{\theta'}(t_k, a^k, o) }}\sqrt{\Delta t_k} \ \epsilon}_{\text{Diffusion}} , \quad \epsilon \sim \mathcal{N}(0, \mathbb{I}_{d_A}) \end{align} \]

^* Note: The $ \sqrt{\Delta t_k} $ term is omitted when using uniform discretization, as it is equivalent to scaling $ \sigma_{\theta'} $'s output.
However, the analogy above is just one way to understand our approach, but now how it was invented. Unlike methods that simulate a continuous-time stochastic differential equation (SDE), which need very small steps to avoid errors, ReinFlow models the flow policy as a discrete-time process during inference. This allows it to fine-tune with fewer denoising steps while still accurately evaluating probabilities.
How does ReinFlow differ from diffusion?
- ReinFlow still retains a deterministic component (the velocity) obtained from pre-training.
- Noise is introduced only during fine-tuning, recovers an ODE after fine-tuning.

ReinFlow: Fine-tuning Flow Matching Policy with Online Reinforcement Learning